What is ANOVA?

Analysis of variance (ANOVA) is a statistical tool that is used to verify the mean of two or more than two groups that are significantly different from each other. ANOVA is used to check the significance of one or more factors by comparing the means of different parameters. This tool is used to analyse the variation present in an experiment.

To use ANOVA, we need to have:

• A continuous variable (e.g., mobile usage) as the dependent variable
• A categorical or nominal variable that has at least two independent groups (e.g.: Age groups: 5-15, more than 15) as the independent variable.

If we have two parameters (or groups), then we can use T-test to test the difference between means is significant or not. When there are more than two parameters, then using T-test may become unreliable. In this case, ANOVA is much more effective in determining significant group differences. T-test compares mean between two independent groups. ANOVA compares mean between more than two independent groups. 

Why ANOVA and not T-test

ANOVA preserves the significance level. 

Example 1: Assume there are 3 groups namely A, B, C to be compared and we decide to do T-test. Number of T-test to be done: 3 T-tests (A with B, B with C, and A with C). Let alpha (error rate) = 5% for each T-test. At an error rate of 5% each test, we have an overall chance of up to 1- (0.95)³= 14% of making an error (if all 3 comparisons were independent).

Example 2: If we want to compare 6 groups, we will have to do 15 pairwise T-tests. This would give us a high chance of finding something significant just by chance. With alpha = 5% for each T-test, probability of error = 1- (0.95)¹⁵ = 54%.

Homogeneity of Variance

The ideal conditions are

•  Equal sample sizes in each group.
•  An equal amount of variation (e.g., the standard deviation) in each group.
•  If the sample sizes and the standard deviations are quite different in various groups, there is a problem.

How ANOVA is calculated?

• The ANOVA test is based on the F- ratio
• F ratio is the ratio between variation due to an experimental treatment and variation due to experimental error.
• Null hypothesis: F ratio = 1.0, or the treatment effect is the same as the experimental error.

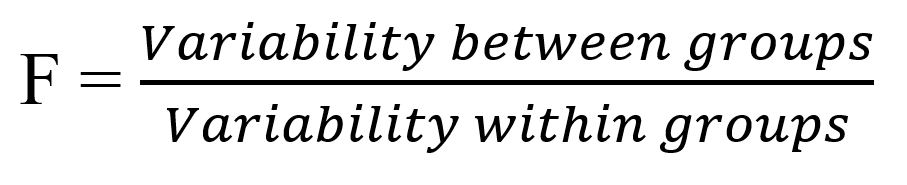
• After an observed F value (F₀) is determined, we need to check the table that lists critical values for F associated with different alpha level.
• Using the degrees of freedom, we can check if our observed value (F₀) is larger than the critical value (F_c).
• If F₀ > F_c, then the F value is statistically significant.
• We can conclude that the difference between group mean is large enough to not due to chance.

One-way ANOVA test

• It is an extension of the 2 sample t-test and is used to determine if there are differences among > 2 group mean.
• One-way ANOVA allows us to compare the mean of two or more groups (independent variable) on one dependent variable to determine if the groups mean differ significantly from one another.

Assumptions:

• Groups must be independent samples
• Normality within each group
• Equal variances within group

Example: To test the effect of various exercises on weight loss. Assume there are 5 different exercises E1, E2, E3, E4, and E5. 20 men were selected and assigned 4 exercises to each of them. After few weeks the weight loss was recorded.

Explanation: It is one-way balanced ANOVA because we have only one category (ie. exercise program). It is balanced because we have exactly same number of men on each exercise program.

Two-way ANOVA test

Example: Assume that we have 5 categories of exercises E1, E2, E3, E4 and E5 and 4 categories of diets Diet1, Diet2, Diet3 and Diet4. Say that 4 persons were selected for each exercise and category. There will be 5x4x4=80 men.

Explanation: It is two-way crossed balanced ANOVA because we have categorized men in two ways: exercises and diets. This model is also balanced as we have the exactly the same number of men for each exercise diet.

Hope, this article would help you to know about what is ANOVA and how to conduct an ANOVA test.

Watch: iLovePhD Videos